2023/03/04(土)修整:Problem#solve_dfsとProblem#dfsを高速化
2023/03/06(月)修整:Questionクラスをリファクタリング
目次
多重ループを避ける方法
Ruby で多重ループを避ける方法には、Array#productを使う方法があります。
しかし、この方法では不要な計算をスキップすることができません。
そこでおすすめするのが深さ優先探索 (バックトラック法, DFS)です。
この方法では、ループをネストする代わりに再帰 関数を呼び出すことで多重ループを避けることができます。
この記事では、覆面算を解くプログラムを例に長大な10重ループを小さな再帰 関数に書き換える様子をお見せします。
覆面算とは
覆面算とは数字の代わりにアルファベットが書かれた筆算の式が与えられ、そのアルファベットに当てはまる数字を当てるというものです。
有名な例は、以下になります。
SEND
+) MORE
--------
MONEY
ちなみに、答えは以下のようになります。
9567
+) 1085
--------
10652
覆面算の解き方
覆面算では、問題がアルファベットの式で与えられます。
それぞれのアルファベットには、数字の0~9が当てはまります。
これを総当たりで解こうとすると、各アルファベットごとに0~9の数字をそれぞれ試すことになります。
そのため、使われているアルファベットの数だけのループ処理が必要になります。
例題のSEND+MORE=MONEYでは8つのアルファベットが使われているので0~9の繰り返しが8重必要になります。
実際には、異なるアルファベット同士で同じ数字になることはないため、そのときには繰り返しをスキップ(next)できます。
また、最大10重ループ必要ですが8重ループで済むときには、9重ループ目以降はループを飛ばす(break)ことができます。
まず、覆面算を解くプログラム中の10重ループを抜き出したコードが以下になります。
各ループ中では、特定の条件に合致したらループを飛ばしたり(break)、次の繰り返しにスキップ(next)したりして、ループ数を減らしています。
def solve
(0 ...10 ).each do |x0|
next if @table [0 ][:head? ] and x0 == 0
@table [0 ][:num ] = x0
(0 ...10 ).each do |x1|
next if x0 == x1
next if @table [1 ][:head? ] and x1 == 0
@table [1 ][:num ] = x1
(0 ...10 ).each do |x2|
next if [x0, x1].include?(x2)
next if @table [2 ][:head? ] and x2 == 0
@table [2 ][:num ] = x2
answer if @table .size == 3
(0 ...10 ).each do |x3|
break if @table .size == 3
next if [x0, x1, x2].include?(x3)
next if @table [3 ][:head? ] and x3 == 0
@table [3 ][:num ] = x3
answer if @table .size == 4
(0 ...10 ).each do |x4|
break if @table .size == 4
next if [x0, x1, x2, x3].include?(x4)
next if @table [4 ][:head? ] and x4 == 0
@table [4 ][:num ] = x4
answer if @table .size == 5
(0 ...10 ).each do |x5|
break if @table .size == 5
next if [x0, x1, x2, x3, x4].include?(x5)
next if @table [5 ][:head? ] and x5 == 0
@table [5 ][:num ] = x5
answer if @table .size == 6
(0 ...10 ).each do |x6|
break if @table .size == 6
next if [x0, x1, x2, x3, x4, x5].include?(x6)
next if @table [6 ][:head? ] and x6 == 0
@table [6 ][:num ] = x6
answer if @table .size == 7
(0 ...10 ).each do |x7|
break if @table .size == 7
next if [x0, x1, x2, x3, x4, x5, x6].include?(x7)
next if @table [7 ][:head? ] and x7 == 0
@table [7 ][:num ] = x7
answer if @table .size == 8
(0 ...10 ).each do |x8|
break if @table .size == 8
next if [x0, x1, x2, x3, x4, x5, x6, x7].include?(x8)
next if @table [8 ][:head? ] and x8 == 0
@table [8 ][:num ] = x8
answer if @table .size == 9
(0 ...10 ).each do |x9|
break if @table .size == 9
next if [x0, x1, x2, x3, x4, x5, x6, x7, x8].include?(x9)
next if @table [9 ][:head? ] and x9 == 0
@table [9 ][:num ] = x9
answer
end
end
end
end
end
end
end
end
end
end
end
そして、上のコードを深さ優先探索 で書き換えたものが以下になります。
66行のコードがわずか17行にまで減りました。
def solve_dfs
xs = (0 ...10 ).to_a
xs.each do |x|
dfs(0 , x, xs)
end
end
def dfs (i, x, xs)
return if @table [i][:head? ] and x == 0
@table [i][:num ] = x
return answer if i + 1 == @table .size
ys = xs - [x]
ys.each do |y|
dfs(i + 1 , y, ys)
end
end
※覆面算を解くプログラムのソースコード 全体が知りたい方は、下にソースコード を貼っておくので参考にしてみてください。
dfsでは繰り返さない場合には、早期にreturnしています。
dfsの引数xsには配列を渡しています。配列の中の各値xs[i]は、@table[i][:num]に代入しています。
xsには各繰り返しで試しているアルファベットの候補の数字が入っています。
dfsの最後では、0~9の値でループしてdfs自身を再起的に呼び出しています。
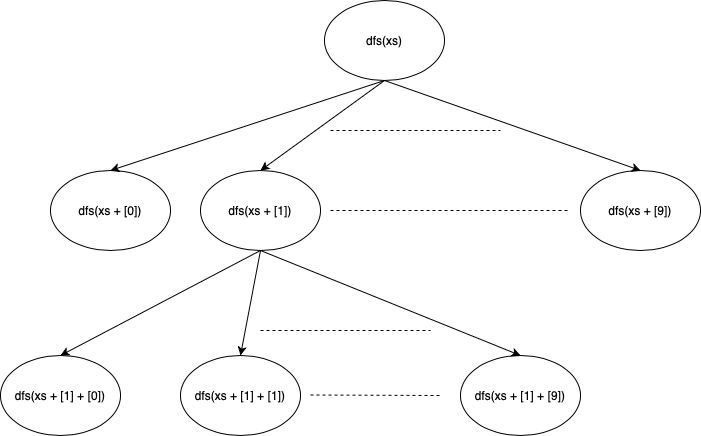
dfsの再帰 の様子を下の図にしました。各dfsでは10回dfsを呼び出しており、その呼び出されたdfsの中でも10回呼び出しています。
深さ優先探索
覆面算を解くプログラムのソースコード 全文
class Object
def deep_clone
Marshal .load(Marshal .dump(self ))
end
end
class Question
REG = /([ a-z ]+)([ +* ])([ a-z ]+) = ([ a-z ]+)/
def initialize (question)
m = REG .match(question)
@expr0 = m[0 ]
@expr1 = m[1 ]
@op = m[2 ]
@expr2 = m[3 ]
@expr3 = m[4 ]
@heads = [@expr1 [0 ], @expr2 [0 ], @expr3 [0 ]].uniq
end
def to_s
@expr0
end
def head? (c)
@heads .include?(c)
end
def answer? (table)
expr1 = expr_str_to_num(@expr1 , table)
expr2 = expr_str_to_num(@expr2 , table)
expr3 = expr_str_to_num(@expr3 , table)
op_lambda.call(expr1, expr2) == expr3
end
def display (table)
printf "\n %15d \n" , expr_str_to_num(@expr1 , table)
print "#{ @op } ) "
printf " %13d \n" , expr_str_to_num(@expr2 , table)
puts " ----------------- "
printf " %15d \n" , expr_str_to_num(@expr3 , table)
end
private
def expr_str_to_num (expr_str, table)
expr_str
.each_char
.map { |c|
table
.find { |letter| letter[:name ] == c }
.fetch(:num )
}
.join("" )
.to_i
end
def op_lambda
case @op
when " + " then ->(x, y) { x + y }
when " * " then ->(x, y) { x * y }
end
end
public
class << self
def valid? (question)
max_ten_char = question
.each_char
.select {|c| /[ a-z ]/ .match?(c) }
.uniq
.size <= 10
REG .match?(question) and max_ten_char
end
end
end
class Problem
def initialize (question)
@question = Question .new(question)
@table = Problem .make_table(@question )
@answers = []
end
def solve_dfs
xs = (0 ...10 ).to_a
xs.each do |x|
dfs(0 , x, xs)
end
end
def dfs (i, x, xs)
return if @table [i][:head? ] and x == 0
@table [i][:num ] = x
return answer if i + 1 == @table .size
ys = xs - [x]
ys.each do |y|
dfs(i + 1 , y, ys)
end
end
def solve
(0 ...10 ).each do |x0|
next if @table [0 ][:head? ] and x0 == 0
@table [0 ][:num ] = x0
(0 ...10 ).each do |x1|
next if x0 == x1
next if @table [1 ][:head? ] and x1 == 0
@table [1 ][:num ] = x1
(0 ...10 ).each do |x2|
next if [x0, x1].include?(x2)
next if @table [2 ][:head? ] and x2 == 0
@table [2 ][:num ] = x2
answer if @table .size == 3
(0 ...10 ).each do |x3|
break if @table .size == 3
next if [x0, x1, x2].include?(x3)
next if @table [3 ][:head? ] and x3 == 0
@table [3 ][:num ] = x3
answer if @table .size == 4
(0 ...10 ).each do |x4|
break if @table .size == 4
next if [x0, x1, x2, x3].include?(x4)
next if @table [4 ][:head? ] and x4 == 0
@table [4 ][:num ] = x4
answer if @table .size == 5
(0 ...10 ).each do |x5|
break if @table .size == 5
next if [x0, x1, x2, x3, x4].include?(x5)
next if @table [5 ][:head? ] and x5 == 0
@table [5 ][:num ] = x5
answer if @table .size == 6
(0 ...10 ).each do |x6|
break if @table .size == 6
next if [x0, x1, x2, x3, x4, x5].include?(x6)
next if @table [6 ][:head? ] and x6 == 0
@table [6 ][:num ] = x6
answer if @table .size == 7
(0 ...10 ).each do |x7|
break if @table .size == 7
next if [x0, x1, x2, x3, x4, x5, x6].include?(x7)
next if @table [7 ][:head? ] and x7 == 0
@table [7 ][:num ] = x7
answer if @table .size == 8
(0 ...10 ).each do |x8|
break if @table .size == 8
next if [x0, x1, x2, x3, x4, x5, x6, x7].include?(x8)
next if @table [8 ][:head? ] and x8 == 0
@table [8 ][:num ] = x8
answer if @table .size == 9
(0 ...10 ).each do |x9|
break if @table .size == 9
next if [x0, x1, x2, x3, x4, x5, x6, x7, x8].include?(x9)
next if @table [9 ][:head? ] and x9 == 0
@table [9 ][:num ] = x9
answer
end
end
end
end
end
end
end
end
end
end
end
def display_answers
@answers .each_with_index do |table, i|
printf "\n 正解【%2d】 \n" , i + 1
table.each_with_index do |letter, j|
printf " %10c = %d " , letter[:name ], letter[:num ]
print "\n" if j % 2 == 1
end
@question .display(table)
end
end
private
def answer
@answers << @table .deep_clone if @question .answer?(@table )
end
class << self
def make_problem
loop do
puts " ↓の例のように文字を入力して下さい。 "
puts " 例:send+more=money "
puts " 例:send*sp=money "
print " > "
question = gets.chomp.downcase
return Problem .new(question) if Question .valid?(question)
end
end
def make_table (question)
question
.to_s
.each_char
.select {|c| /[ a-z ]/ .match?(c) }
.uniq
.sort
.map {|c| {name : c, num : 0 , head? : question.head?(c)} }
end
end
end
def main
loop do
p = Problem .make_problem
start_time = Time .now
p.solve_dfs
end_time = Time .now
p.display_answers
printf "\n 計測時間:%.1f秒 \n" , (end_time - start_time)
print " もう一度繰り返しますか?はい…(0)/いいえ…(1): "
break if gets.to_i == 1
end
end
if __FILE__ == $PROGRAM_NAME then
main
end
おわりに
どうでしたか。深さ優先探索 を用いることで多重ループを避ける方法を紹介しました。
ソースコード は、短くなりますが基本的には全探索に近いことをやっているので多重ループの時と計算量は変わりません。
SEND+MORE=MONEYの場合
計算量を抑えることはできませんが、ソースコード を短くできるので皆さんもぜひ多重ループを避けるときには、深さ優先探索 を試してみてください。
ちなみに、この覆面算を解くプログラムは昔C言語 で書いたことがあって、それをRuby に移植したものになります。
最後にgcc -O3でコンパイル したものとの実行速度の比較を下に載せておきます。
C言語 はRuby より実に129.5倍高速でした。
参考